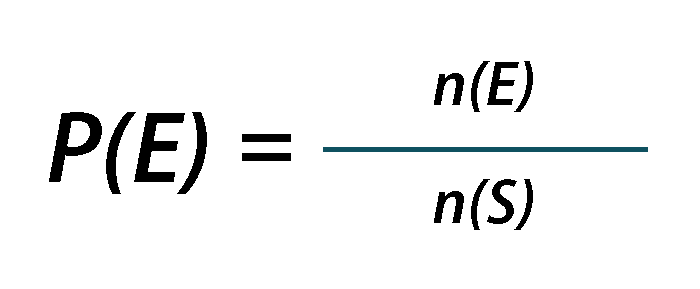Los resultados de los fenómenos aleatorios pueden darnos una idea de la probabilidad de que dichos resultados sucedan. Normalmente este tipo de observaciones tienen que hacerse porque se desconoce casi por completo el fenómeno aleatorio bajo estudio. Sin embargo, existen otras maneras de calcular probabilidades dependiendo del fenómeno que se estudie.

En algunos fenómenos aleatorios, como las cuestiones climatológicas o el comportamiento de las camadas de gatitos, el análisis sólo puede darse en términos de tendencias y de probabilidades frecuenciales, ya que lo único con lo que se cuenta es con alguna información de cómo se ha comportado el fenómeno aleatorio. Pero existen casos con más información.

Si tomamos un dado de seis caras y lo lanzamos para observar qué valor queda hacia arriba, tendremos un fenómeno aleatorio. Podríamos realizar lanzamientos sucesivos para darnos una idea de qué probabilidad tiene cada cara de aparecer. Por la forma en la que está construido el experimento, realizar repeticiones puede no ser necesario.

El dado consta de seis caras iguales, por lo que la intuición indica que podríamos esperar una tendencia de aparición igual para cada cara. Es decir, al lanzar el dado una y otra vez puede esperarse que cada cara aparezca, aproximadamente, en una sexta parte de los lanzamientos. Dicho más formalmente, en total se tienen seis posibles resultados, todos igualmente probables, por lo que cada uno de ellos ofrecerá una probabilidad de aparecer de un sexto o 0.167 aproximadamente.

Esta idea puede tomarse como una interpretación de lo que se conoce como:

Definición Clásica de Probabilidad. Básicamente nos dice que si tenemos un fenómeno aleatorio del cual conocemos todos sus posibles resultados, entonces es viable calcular la probabilidad de ocurrencia de uno de ellos o de la combinación de algunos de ellos, dividiendo el total de formas en las que puede ocurrir el resultado deseado entre el total de posibles resultados del fenómeno aleatorio.

Partiendo del hecho de que se está analizando un fenómeno aleatorio, llamaremos experimento a cada repetición de dicho fenómeno.

A aquel resultado o aquella combinación de resultados del experimento cuya probabilidad de ocurrencia nos interese medir, le llamaremos evento.

Una probabilidad de 0.17 para un evento puede expresarse también como una probabilidad de 17%, e indica que si repitiéramos el experimento 100 veces, podríamos esperar que el evento sucediera en 17 de esas 100 veces.

De acuerdo con esto y con la idea de la definición clásica de probabilidad que mencionamos, podemos enunciar ahora más formalmente:

Dado un experimento cuyo número total de posibles resultados esté dado por n(S) y sea un evento E de este experimento cuyos posibles resultados son n(E). Entonces la probabilidad de que ocurra E, denotada por P(E), está dada por:

Es decir:

La probabilidad es la razón del número de resultados de éxito respecto al total de resultados posibles.

La fórmula de la probabilidad clásica es la siguiente:

Veamos qué significa esta expresión con un ejemplo.

¿Cuál es la probabilidad de que una persona de 35 años de edad llegue a sobrevivir hasta que tenga 50 años, si de acuerdo a una tabla de mortalidad de cada 83745 personas de 35 años, 67426 llegan a los 50 años?

Esta probabilidad puede expresarse como un porcentaje si la multiplicamos por 100:

0.8051 x 100=80.51%

El 80.51% de las personas de 35 años llegará a los 50 años.

Veamos otro ejemplo:

En una bolsa hay 10 canicas de colores, tres rojas, dos verdes y cinco amarillas. Si se extrae una canica al azar. ¿Qué probabilidad hay que sea verde o amarilla?