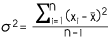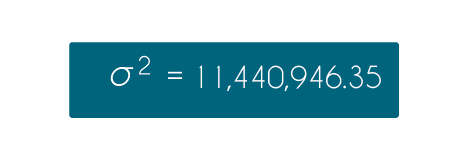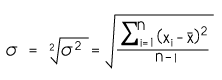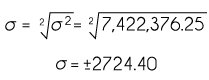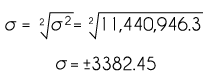El uso de las medidas de tendencia central (media, mediana y moda) permiten describir el comportamiento de un conjunto de datos, sin embargo, existen otro tipo de medidas que nos hablan de la variación entre ellos; en estadística, se utilizan las medidas de dispersión o variabilidad. Las de uso más extendido son el rango, la varianza y la desviación estándar.

Si bien el rango es una medida de dispersión fácil de calcular, nos da una idea general del intervalo de variación de nuestros datos, adolece de ser una medida en términos absolutos. Se calcula como

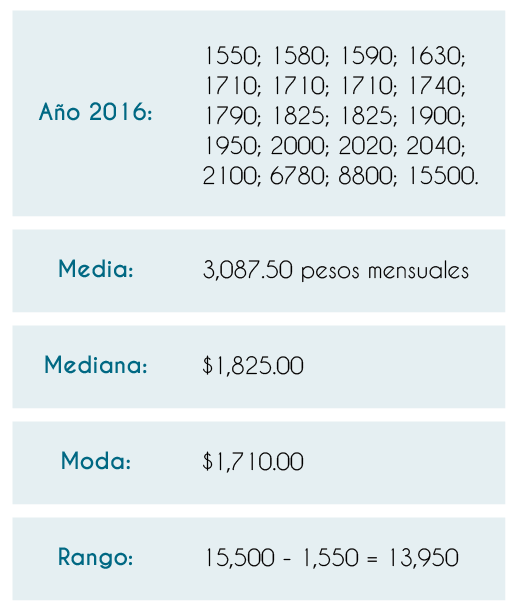
Rango: Valor máximo - valor mínimo

Los datos siguientes muestran los ingresos de las familias para los años 2014 y 2016.

Al obtener los datos de tendencia central, podemos ver que en promedio, en los dos años se tiene el mismo ingreso pero existe más variación en el año 2016. La siguiente medida de variabilidad es la varianza, esta nos indica que tan alejados se encuentran los datos de la media elevados al cuadrado, de esta manera se obtiene una métrica en términos de distancia. La varianza es la media de las diferencias con la media elevadas al cuadrado. Para calcularla debemos seguir los pasos siguientes:

1. Calcula la media de los datos.
2. Ahora, a cada valor de nuestros datos debes restar la media y el resultado lo elevas al cuadrado (la diferencia elevada al cuadrado).
3. Ahora calcula la media de esas diferencias al cuadrado.

De tal forma que la fórmula¹ es:

¹ Cuando el número de datos es menor a 20, la fórmula lleva n-1 en el denominador

Calculemos la varianza para los ingresos de los años 2014 y 2016.

Año 2014: 1700; 1730; 1740; 1750; 1790; 1800; 1850; 1900; 1950; 2025; 2025; 2100; 2170; 2220; 2300; 3000; 3700; 4900, 8000, 13100.

Media: 3,087.50

Tú puedes realizar paso a paso cada una de las operaciones para 2016, nosotros sólo te mostraremos el resultado

Para ser más precisos en la descripción de los ingresos se recomienda la desviación estándar. Entre sus propiedades se tiene:

1. Es una medida de variación de todos los valores con respecto a la media
2. Su valor siempre es positivo o cero.
   • Si es cero, significa que todos los datos son el mismo número.
   • Si su valor es pequeño significa que los datos son muy cercanos o parecidos entre sí.
   • Si, por el contrario, su valor es grande, quiere decir que hay grandes variaciones entre los datos.
3. Al igual que en las medidas de tendencia central, sus unidades son las mismas que las de los datos originales; no sucede así en la varianza, cuyas unidades son las de los datos originales, pero elevadas al cuadrado.

Para calcular la desviación estándar primero debemos calcular la varianza.

Para nuestro caso, la desviación estándar de 2014 es:

Con los resultados obtenidos podemos decir del 2014.

Para el año 2016, la desviación es estándar es:

Con estos datos podemos decir que en el 2014, los salarios se alejaban de la media en 2,724.40 pesos, mientras que en el 2016, los salarios se alejaban en 3,382.45 pesos. En conclusión, la dispersión de los datos era menor en 2014.

Autoevaluación

Para fortalecer tus aprendizajes, te invitamos a que resuelvas el siguiente reto.

Calcula la media, el rango, la varianza y la desviación estándar. Arrastra los valores a las medidas de dispersión correspondientes.