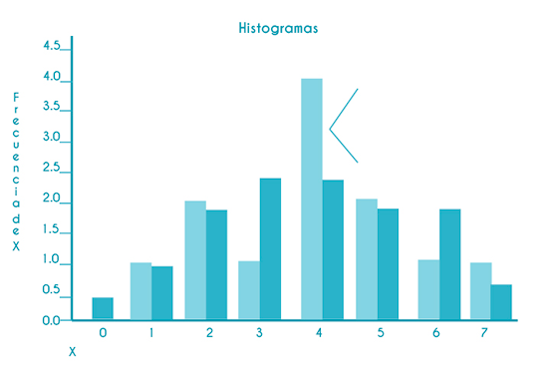
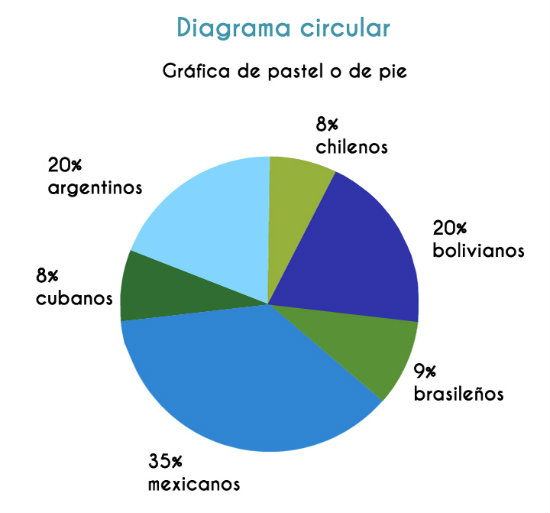
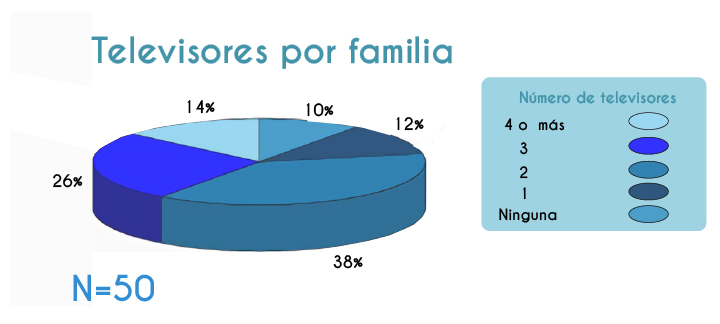
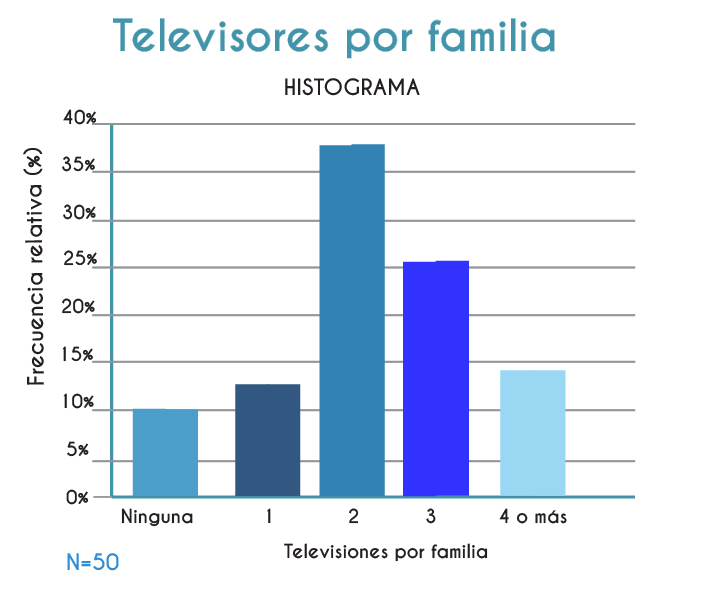
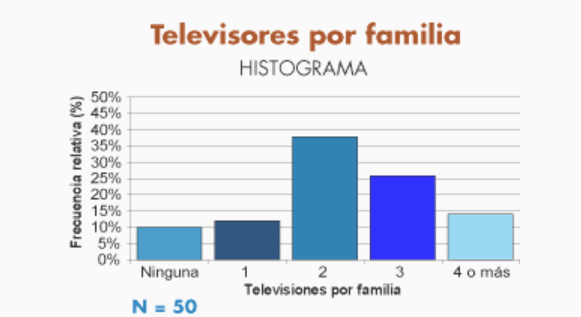
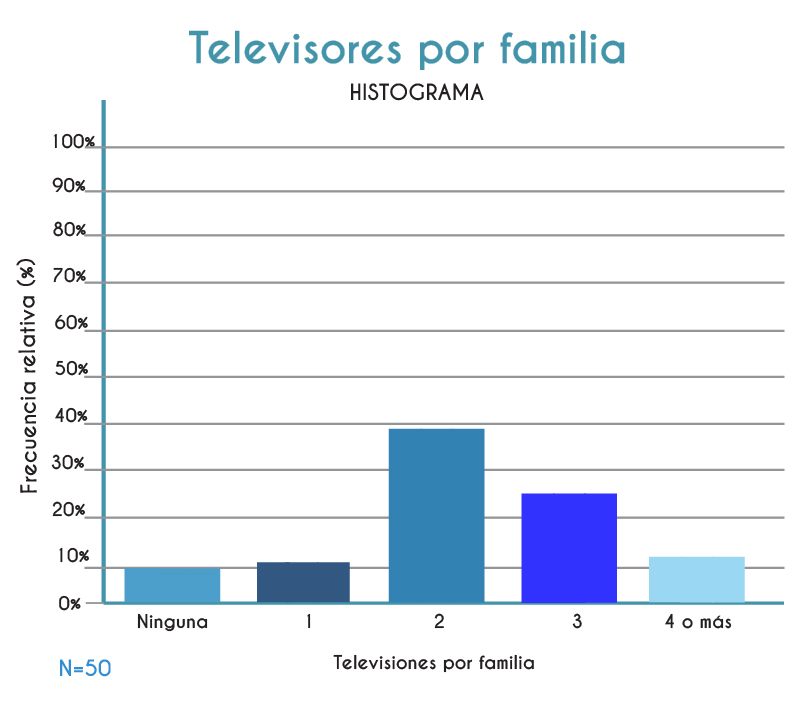
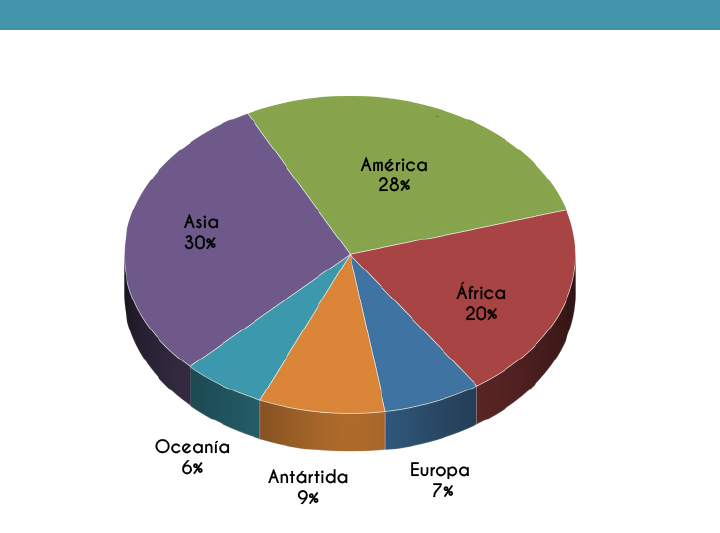
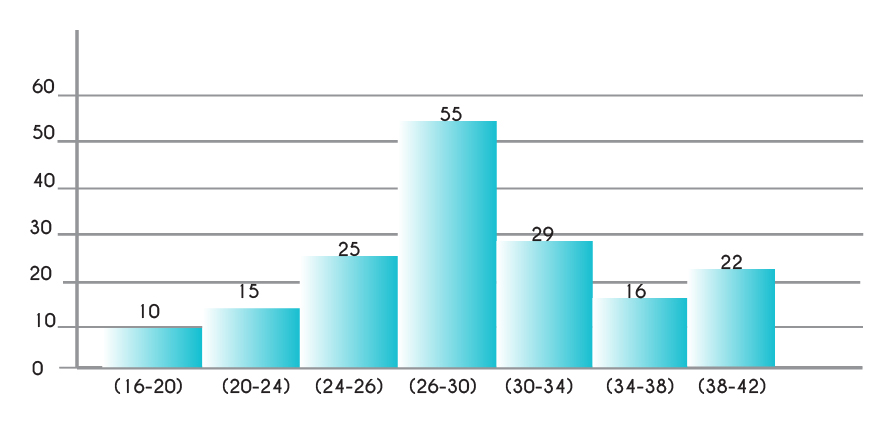
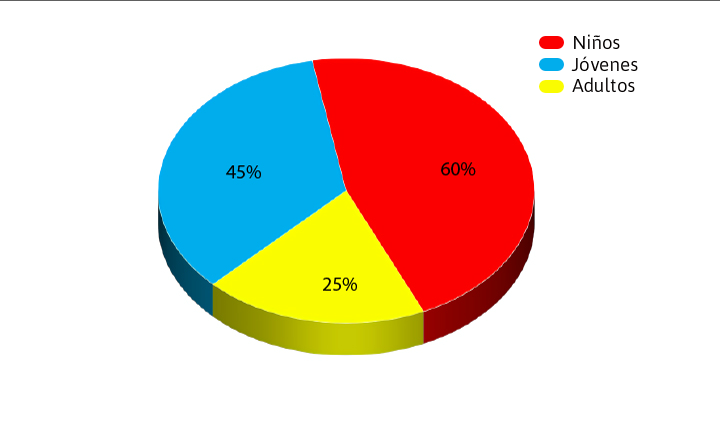
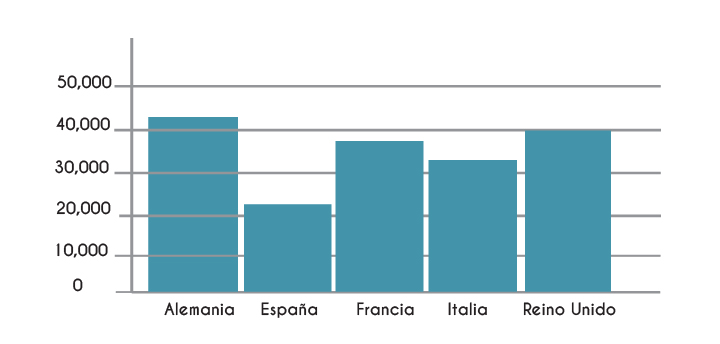
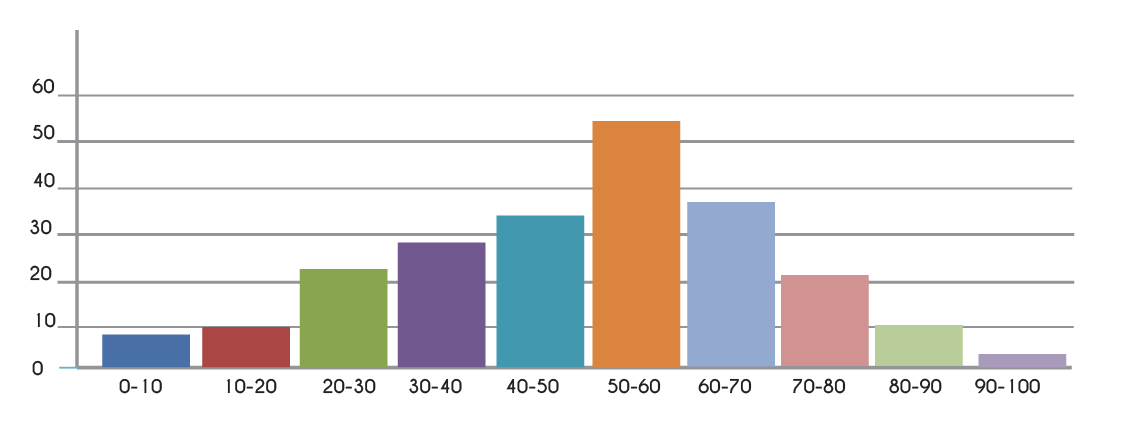Las representaciones gráficas son muy importantes porque nos permiten visualizar la información de manera rápida. Los gráficos se generan a partir de los datos ya sea como listas de ellos o de manera agrupada. Las gráficas más comunes son las gráficas de barras, de pastel o de líneas. Depende su uso deberás decidir por una u otra.

Es importante que recuerdes que cuando trabajamos con datos, la mayor parte del tiempo tenemos una gran cantidad de ellos, y además buscamos que así sea porque mientras más respuestas tengamos (y mayor sea la muestra), podremos plantear generalizaciones más certeras del comportamiento de la población en su conjunto.

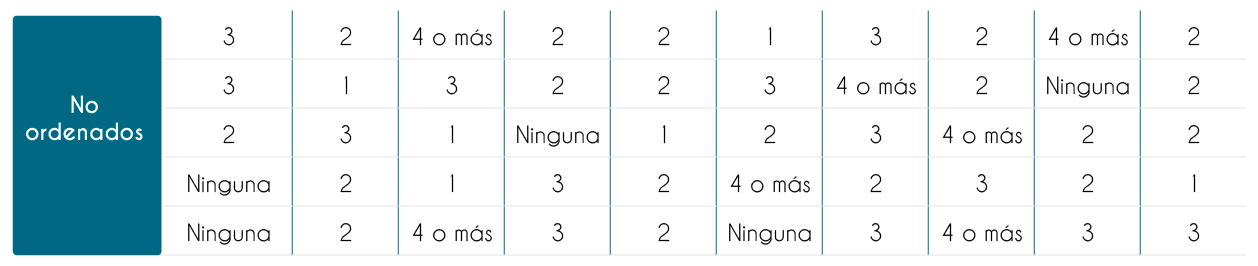
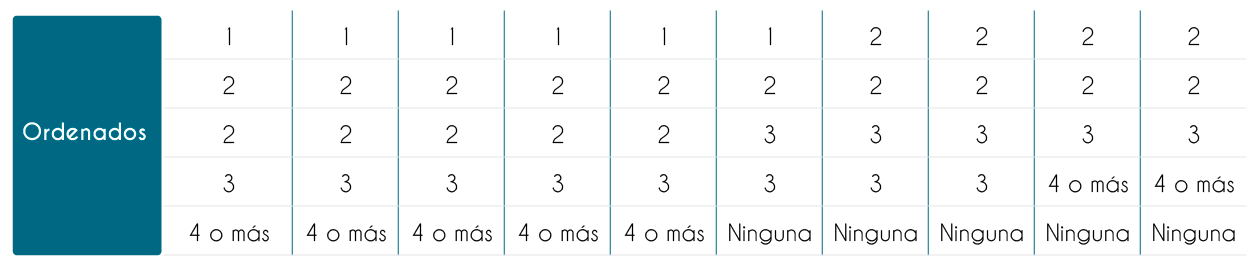
Cuando la cantidad de datos es grande debemos buscar cómo agrupar la información para que sea manejable, y ello se logra con dos tipos de herramientas: las distribuciones de frecuencias (simples y agrupadas) y las representaciones gráficas.

En estadística se denomina distribución de frecuencias a la tabla de datos en que se concentran las diferentes respuestas recabadas y el número de veces que se repiten, o sea, su frecuencia. En cuanto a las representaciones gráficas, aunque hay varias que pueden utilizarse, aquí revisaremos dos:

La distribución de frecuencias aportará los datos para que pueda generarse la representación gráfica, cuya importancia radica, en ser un apoyo visual que proporciona una idea clara y sintética de cómo se comporta una variable. Así que aprendamos a obtener las distribuciones de frecuencias, tanto simples como agrupadas.

Distribución de frecuencias simple

Imagina que aplicamos una encuesta para determinar la influencia de la televisión en la vida familiar y que una de las preguntas del cuestionario es:

Si entrevistamos a 50, 100 ó 1000 personas, sólo pueden optar por una de estas cinco respuestas. Pero ¿te imaginas un listado con tantos datos? Aun cuando usemos una computadora, visualizar la información resultaría muy engorroso. En casos como éste podemos apreciar las ventajas de concentrar la información en una tabla de frecuencias.

Cuando el número de posibles respuestas es reducido, como en nuestro ejemplo en que sólo tenemos 5, lo conveniente es utilizar una distribución de frecuencias simple, o sea, una tabla en la que cada respuesta constituirá una categoría a la que le asociaremos su frecuencia.

Por el momento trabajemos con las 50 respuestas recabadas por un encuestador para la pregunta del número de televisiones.

Ordenamos los datos para que sea más fácil contarlos²

²Aquí vamos a contarlos porque son pocos datos, pero te sugerimos que trates de usar Excel para hacer los cálculos.

Vamos a llenar la tabla con la información anterior

Para las frecuencias relativas, dividir el número de veces entre el total de datos y multiplicarlo por 100. Para las frecuencias acumuladas, debes ir sumando con el anterior.

Aprovecharemos los resultados de nuestra tabla de distribución de frecuencias simples para generar algunas gráficas. Primero, elaboraremos un diagrama de pastel usando la columna Frecuencia relativa para obtener la distribución proporcional y la columna Respuestas para identificar a qué categoría corresponde cada rebanada.

Observa que en la gráfica de pastel tenemos que:

1. La gráfica tiene título, cada porción tiene un color distinto y el porcentaje que representa.
2. Hay un cuadro que indica lo que representa cada porción.
3. Se incluye el tamaño (N=50) de la muestra, que es importante porque permite que las personas que reciben la información tengan idea de qué tan amplia fue nuestra consulta, y por tanto en qué medida podría generalizarse.

La manera más usual o común de presentar una distribución de frecuencias en estadística es mediante las gráficas de barras, conocidas como Histogramas. Cada barra representa la frecuencia de una categoría o respuesta de la encuesta. Las barras se dibujan de manera contigua. Los histogramas nos permiten visualizar la forma que toma la distribución de frecuencias. Elaboremos el histograma de nuestro ejemplo.

• En el eje de las abscisas (que corresponde a la variable independiente) colocaremos las categorías Televisores por familia.
• En el eje de las ordenadas (que corresponde a la variable dependiente) tendremos la frecuencia (generalmente usamos la relativa).

El histograma nos queda así:

Otro aspecto importante:

Tanto al leer como al graficar histogramas es importante tener en cuenta el efecto de la escala vertical. En el histograma que acabamos de ver puedes observar que la escala del eje de las ordenadas varía entre 0 y 40%, ya que en este rango de valores varían nuestras cinco categorías. Sin embargo, también podríamos variar esta escala para que llegara hasta el 50%, el 100% o cualquier valor intermedio entre ellos. Observa lo que pasa entonces:

Autoevaluación

Para verificar sus aprendizajes, te invitamos a realizar el siguiente reto.

Observa detenidamente, arrastra el la descripción que se adecue a las gráficas siguientes.