La función seno
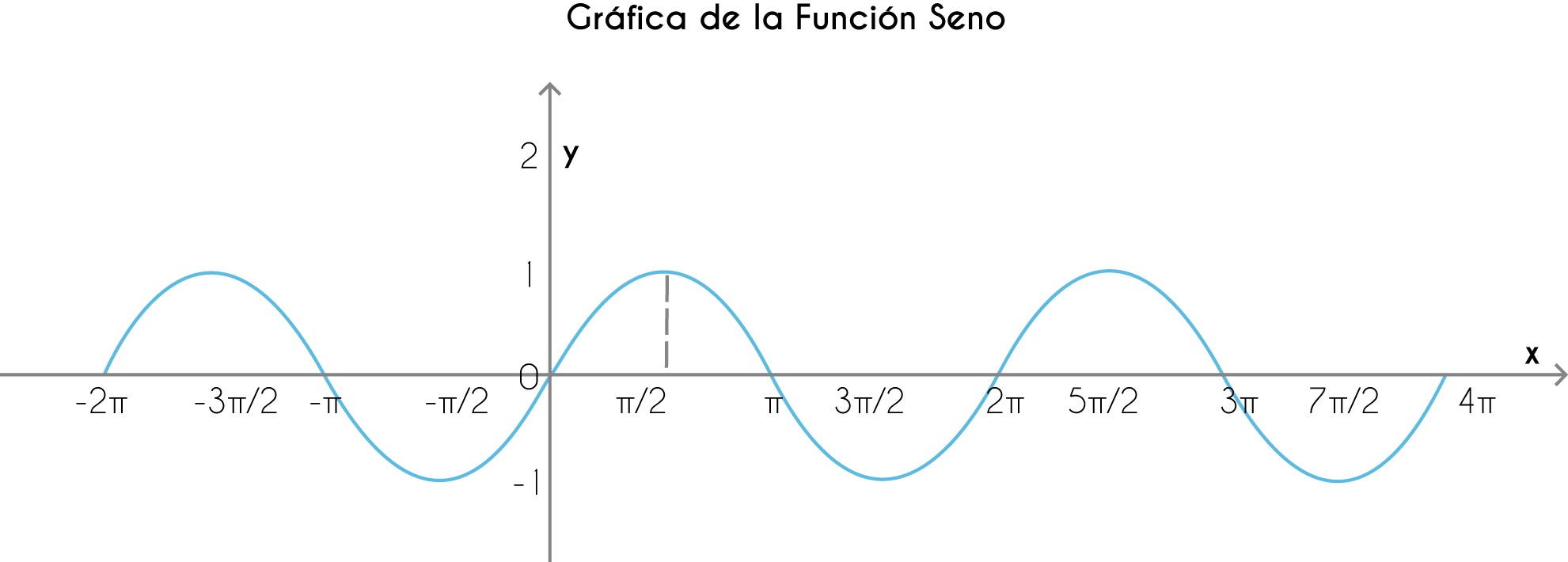
La función seno, $f(x)=sen\:x$ es una función definida para todos los números reales y sus imágenes son también números reales. Su gráfica es una curva llamada senoide o sinusoide que se repite en cada intervalo de longitud $2\pi.$ Matemáticamente, esto significa que $$sen\:(x+n2\pi)=sen\:x$$ con $n$ un número entero, decimos entonces que esta es una función periódica de periodo $2\pi.$
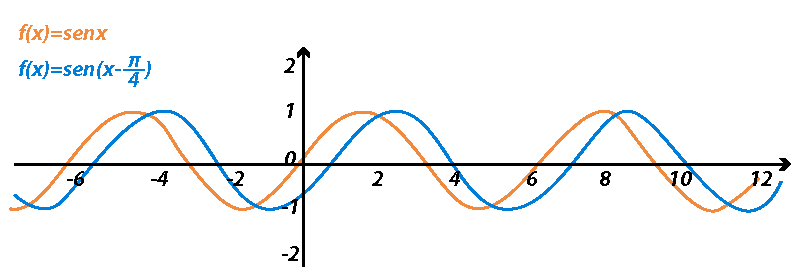
Es decir,
$$sen\:x = sen\:(x+ 2\pi)=$$ $$sen\:(x- 2\pi)= sen\:(x+ 4\pi)=$$ $$sen\:(x-6\pi)=sen\:(x+8\pi)=...$$Notemos que como la función repite los valores que toma en cada periodo, significa que su rango o imagen no es todo el conjunto de reales sino solamente un subconjunto. Como puedes observar en la gráfica la imagen de $f$ es el intervalo $[-1,1]$ pues todos los valores que la función toma, están ahí. Este conjunto se distingue claramente en el eje $y.$
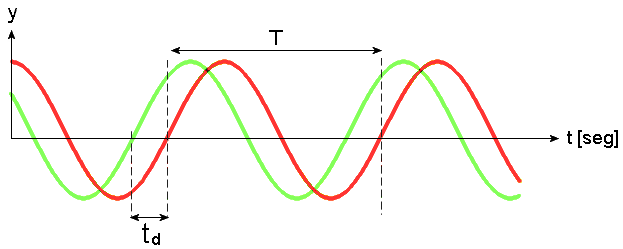
La función seno es muy usada en Física pues con ella se modelan un sinnúmero de fenómenos, los fenómenos físicos periódicos.. Estos fenómenos se modelan matemáticamente usando funciones senoidales -transformaciones de la función seno- porque cambian periódicamente con el tiempo, por ejemplo los movimientos ondulatorios o las señales electromagnéticas.
Entonces dependiendo del fenómeno a modelar se construye la función que lo describe. Tenemos así, una familia infinita de funciones senoidales -sinusoidales- cada una de ellas definida mediante una colección de cuatro valores reales $a, b, c$ y $d,$ sus parámetros.
La familia de funciones senoidales queda descrita mediante la siguiente expresión general: $$f_{abcd}(x)= a\:sen\:(bx+c) + d$$ Donde, los valores de los cuatro parámetros están dados por las condiciones específicas del fenómeno a modelar. Observa que para la función $f(x)=sen\:x$ se tiene que $a=b=1$ y $c=d=0.$