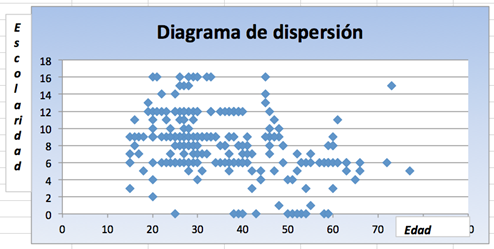
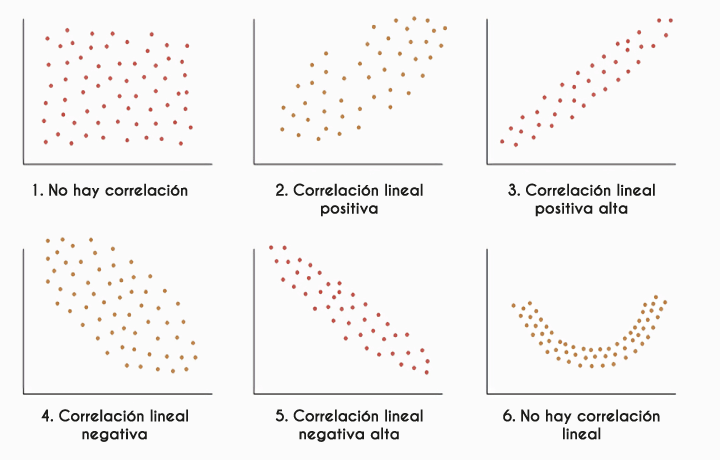
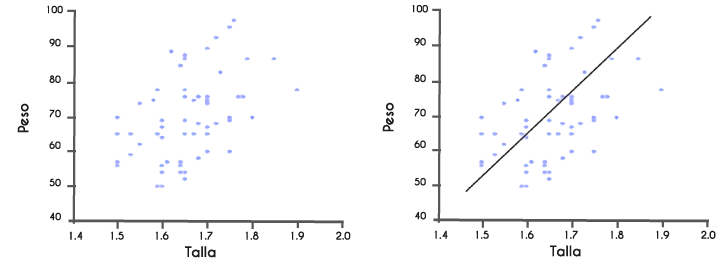
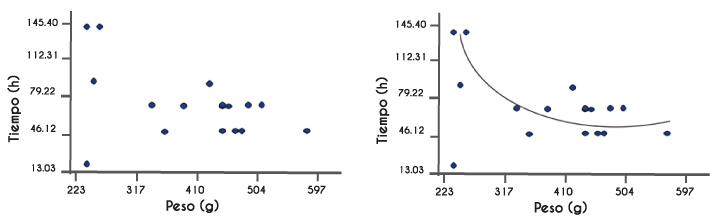
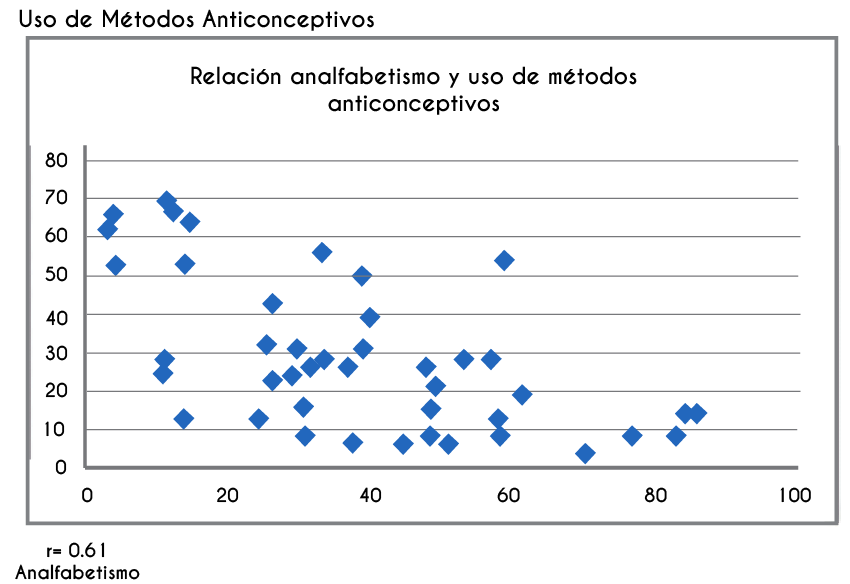
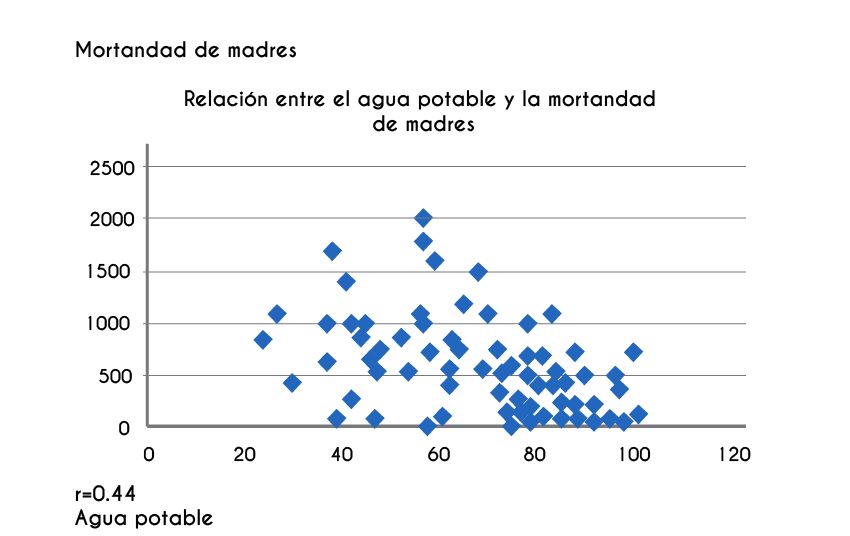
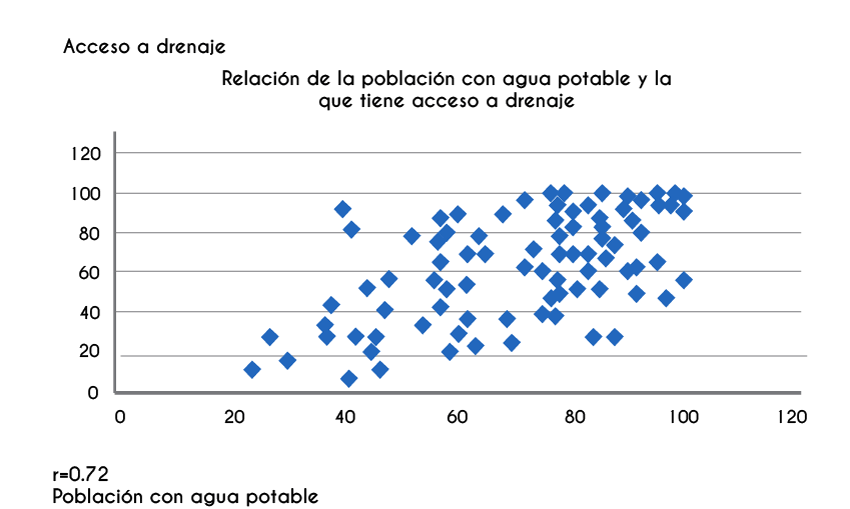
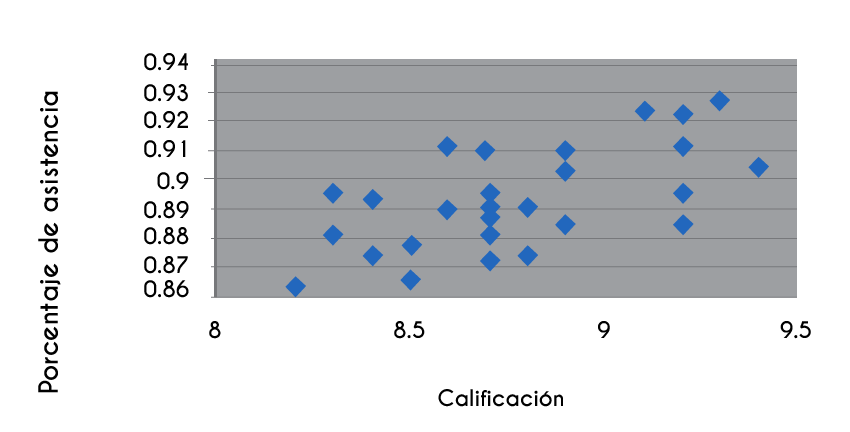
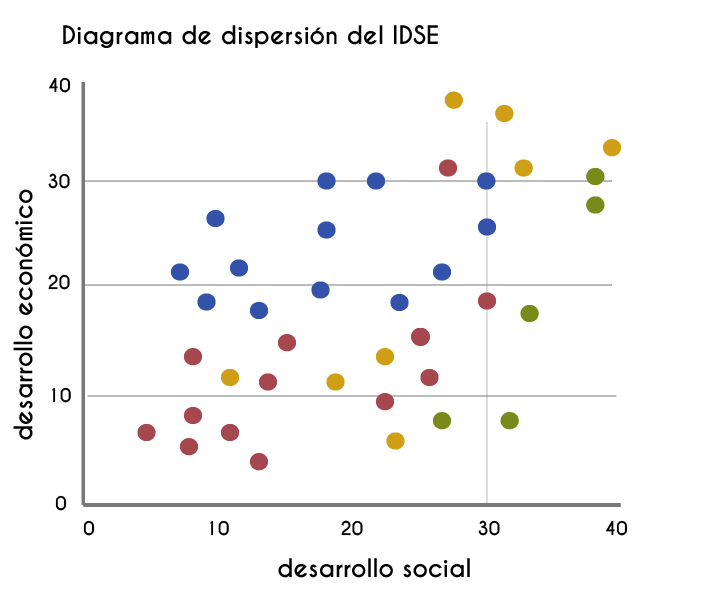
En el caso del estudio de dos variables cuantitativas, la gráfica es muy importante, porque de manera visual podremos determinar en una primera etapa si es posible pensar en una correlación entre las variables, y en ese caso determinar qué modelo matemático es el más adecuado para representar dicha relación. De la misma manera, la observación de la gráfica podría indicarnos la falta de relación entre las variables. La gráfica en la que se representan las parejas ordenadas se conoce con el nombre de diagrama de dispersión.

Pensemos en una encuesta aplicada a los migrantes, en donde además del género y el estado civil, se preguntó acerca de la edad y los años de escolaridad (a partir de la primaria). Estas dos variables son de tipo cuantitativo, es decir, dan una medida numérica de estas características, por lo que las respuestas recabadas son números. Es decir, si una persona contestó que su edad es de 25 años y que cursó 6 años de escuela, estos datos pueden ser representados así: (25,6), ¿a qué te recuerda esta notación?. ¡Claro!, es la manera en que se representan las coordenadas de un punto, para luego graficarlas en un plano cartesiano bidimensional. Así pues, cada pareja de datos que proviene de la misma fuente queda representada gráficamente como un punto.

Recordemos que la idea de trabajar los datos de manera bivariada es buscar la posible relación entre dos variables, de manera que al conocer el valor de una, nos sea posible predecir el valor de la otra. Generalmente, cuando se forman las parejas ordenadas se acostumbra poner primero a la variable que puede controlarse o medirse con mayor facilidad (lo que en funciones llamamos la variable independiente), y luego la variable que querríamos predecir (y que tú conoces del estudio de funciones como variable dependiente).

Con base en la información sobre edad y escolaridad tenemos el siguiente diagrama de dispersión

Un ejemplo más

En 2013 se publicó un estudio realizado en la Comunidad Ch'ol del Estado de Chiapas, en el cual se analizó si hay diferencia en el aprendizaje logrado por estudiantes de 5° y 6° de primaria a quienes se les enseña en la escuela con un idioma diferente al materno, ya que las clases son en español y la lengua materna es el Ch’ol. Para esto se aplicó un examen de 10 preguntas, primero en su lengua materna y 24 horas después en español. Como hipótesis se esperaba que los niños obtuvieran mejores calificaciones en el examen aplicado en Ch'ol, que es su lengua materna.

Los resultados obtenidos se pueden apreciar en esta gráfica:

Fuente: Bastiani, J., et al. (2013). Medición de conocimientos con reactivos en Ch'ol y Español en niños de educación básica con modelos pedagógico intercultural bilingüe. Revista Electrónica de Investigación Educativa, 15(1), 107-121. Recuperado el 16 de octubre de 2013 en http://redie.uabc.mx/vol15no1/contenido-bastianietal.html

Observa que la Variable independiente es la calificación obtenida en el examen aplicado y es como máximo 10. En tanto que la Variable dependiente es la calificación obtenida en el curso regular, llamado en el estudio índice de calificación escolar.

También puedes ver que las gráficas nos muestran con una cruz los resultados obtenidos cuando el examen se aplicó en español y con un círculo blanco cuando el examen se aplicó en Ch'ol. ¿Crees que hay correlación entre las calificaciones obtenidas en el examen de conocimientos y el índice de calificación escolar? ¿Cómo puedes interpretar la gráfica?

En estadística, el análisis y la interpretación de los datos son muy importantes, y este puede hacerse a través de una técnica que se conoce como regresión lineal, en donde los diagramas de dispersión son muy importantes pues nos permiten conocer el comportamiento de los datos.

Al construir el diagrama de dispersión de los datos establecemos la variable que consideraremos independiente (o sea, qué variable mediremos) y la variable dependiente (es decir, aquella que queremos predecir o estimar usando un modelo lineal). La construcción del diagrama de dispersión es muy importante porque visualmente podemos determinar si un conjunto de datos podría representarse mediante una recta o no. Observa los siguientes diagramas:

Como puedes ver en las gráficas 1 y 6 no hay correlación lineal. En el caso 1, no se ve que haya un patrón de comportamiento especial en los puntos: a simple vista no se visualiza qué efecto produce la variable independiente sobre la dependiente. En el caso 6 en cambio, sí se ve un comportamiento definido, una correlación, pues los puntos forman una parábola. El diagrama de dispersión nos ha permitido visualizar la correlación clara, y también nos deja claro que dicha correlación no es de tipo lineal sino cuadrático.

En cambio, en los casos 2 y 3, la distribución de los puntos hace pensar que podemos trazar una recta que pase aproximadamente a la misma distancia de la mayoría de los puntos.

Observa entonces que el diagrama nos ha ayudado a determinar que el conjunto de datos puede ser susceptible de un análisis de correlación lineal. Además, los diagramas nos muestran además que a medida que aumenta el valor de x, también aumenta el valor de y, por lo que podemos hablar de una correlación positiva. Como es natural, hay casos en los que el ajuste entre los puntos y la recta es muy bueno (como el caso 3) y otros casos en los que hay mayor dispersión (como en el caso 2): Los casos 4 y 5 también se pueden visualizar a grandes rasgos como rectas, sólo que ahora el efecto entre las variables es inversamente proporcional, o sea, al aumentar el valor de las abscisas, disminuye el valor de las ordenadas. Esto se llama correlación negativa.

Una manera de hacerlo es pensar en trazar una línea que pase por en medio de los puntos para analizar el comportamiento.

Por ejemplo:

En este caso, en la gráfica de talla y peso, podemos decir que existe una correlación lineal positiva, lo que se traduce en que a mayor talla el peso se incrementa.

La gráfica siguiente muestra a relación entre el peso de un objeto y el tiempo en que tarda en caer

En este caso, existe una correlación negativa y el modelo que mejor ajusta a los datos es una curva exponencial con pendiente negativa. En la interpretación podemos decir que entre más peso se tenga, el tiempo que tarda en caer es menor.

Con base en lo revisado sobre el comportamiento de las variables y representación gráfica, te pedimos llenes la siguiente tabla. Es necesario que revises cuál es la variable que influye (independiente) en el comportamiento de la otra (dependiente). Revisa el comportamiento de los diagramas de dispersión para identificar el tipo de correlación. Observa con detenimiento si es posible que pueda ser un modelo lineal el que mejor explica el comportamiento de las variables.

Correlación positiva Agua potable Sí Analfabetismo Correlación negativa Desarrollo económico No Mortalidad de las madres Sí Desarrollo social Calificación Uso de métodos anticonceptivos Correlación negativa Sí No Población con agua potable Acceso a drenaje Correlación positiva Porcentaje de asistencia Correlación positiva

Gráfico	Variable independiente	Variable dependiente	Tipo de correlación	Es lineal