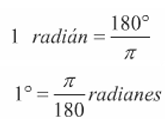El ángulo es la figura formada entre dos rectas que se cruzan en un punto. Las rectas -que podrían también ser semirrectas o segmentos- reciben el nombre de lados del ángulo y el punto donde se cortan es el vértice del ángulo. De hecho, dos rectas que se cruzan forman cuatro ángulos.

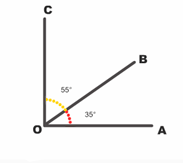
Hay varias maneras de referirnos a un ángulo, podemos darle el nombre del vértice agregando el símbolo de ángulo: $\angle O$, o nombrarlo con una letra griega ($\alpha, \beta, \delta, \gamma, \eta, \epsilon,$ etc.), escrita dentro del ángulo señalándolo con una curva entre las dos rectas. Si el ángulo está determinado por segmentos, podemos identificarlo señalando los puntos que los determinan: el punto central será el del vértice del ángulo y los de los extremos indicarán el sentido en el que lo mediremos. Observa en la siguiente figura,

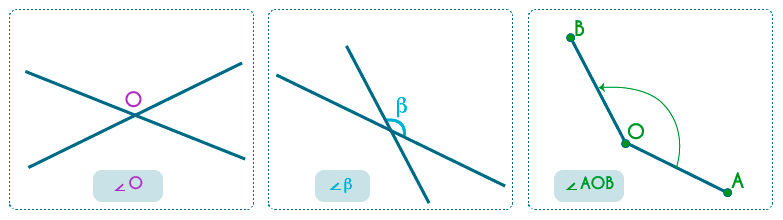
Tenemos el ángulo $\angle O$, el ángulo $\beta$ y el ángulo $\angle AOB$, considerado en sentido positivo es decir, el giro contrario a las manecillas del reloj.

Para medir un ángulo es necesario definir una unidad de medida. Las más usadas son el grado sexagesimal, comúnmente llamado grado, y el radián. El grado sexagesimal es la medida de un ángulo cuya abertura es $\frac{1}{360}$ de la circunferencia. En este caso se considera como vértice del ángulo el centro de la circunferencia y sus lados son dos radios. Por otra parte, para medir un radián también consideramos una circunferencia pero de radio 1. Y nuevamente consideramos el ángulo con vértice en el centro de la circunferencia y cuyos lados son dos radios. La medida del ángulo en radianes será la longitud del arco que el ángulo subtienda en la circunferencia.

La relación que guardan entre sí estas medidas es $$\pi \sim 180°$$ y con ella podemos convertir grados a radianes o radianes a grados. Las expresiones que resultan son:

Los ángulos se clasifican de acuerdo a sus medidas en:

• trending_flatÁngulo recto

  Es el que mide 90º

  
• trending_flatÁngulo llano

  Es el que mide 180º

  
• trending_flatÁngulo perigonal

  Es el que mide 360º

  
• trending_flatÁngulo nulo

  Es el que mide 0º

  
• trending_flatÁngulo agudo

  Es el que mide menos de 90º

  
• trending_flatÁngulo obtuso

  Es el que mide más de 90º y menos de 180º

  

Cuando dos ángulos son adyacentes se clasifican como:

• trending_flatÁngulos complementarios

  Es cuando su suma es igual a 90º

  
• trending_flatÁngulos suplementarios

  Es cuando su suma es igual a 180º

  
• trending_flatÁngulos conjugados

  Es cuando su suma es igual a 360º

  

Como observaste cuando dos rectas se cortan, se forman cuatro ángulos α, β, α', β'. De acuerdo a la figura, podemos ver que α y β son suplementarios, al igual que α' y β'. Los ángulos α y α' son ángulos opuestos por el vértice y también lo son β y β'. Los ángulos opuestos por el vértice tienen la misma medida. Cuando dos ángulos tienen la misma medida se dice que son congruentes. Cuando los ángulos adyacentes α y β miden 90°, cada uno las rectas son perpendiculares

Cuando dos rectas paralelas se cortan por una recta transversal se forman ocho ángulos. Los nombres que se les dan y sus propiedades son las siguientes:

• Ángulos externos son los que se forman fuera de las paralelas: $\angle a, \angle b, \angle g, \angle h$.
• Ángulos internos son los que se forman dentro de las paralelas: $\angle c, \angle d, \angle e, \angle f$.
• Ángulos alternos internos son las parejas de ángulos que se forman dentro de las paralelas y a uno y otro lado de la transversal: $\angle c$ con $\angle f$ y $\angle e$ con $\angle d$. Estos ángulos son congruentes.
• Ángulos alternos externos son las parejas de ángulos que se forman fuera de las paralelas y a uno y otro lado de la transversal: $\angle a$ con $\angle h$ y $\angle b$ con $\angle g$. Estos ángulos son congruentes.
• Ángulos correspondientes son las parejas de ángulos no adyacentes que se forman del mismo lado de la transversal: $\angle a$ con $\angle e$, $\angle c$ con $\angle g$, $\angle b$ con $\angle f$ y $\angle d$ con $\angle h$. Estos ángulos son congruentes.
• Ángulos colaterales internos son los que se forman dentro de las paralelas del mismo lado de la transversal: $\angle c$ y $\angle e$, $\angle d$ y $\angle f$. Estos ángulos son suplementarios.
• Ángulos colaterales externos son los que se forman fuera de las paralelas y del mismo lado de la transversal: $\angle a$ y $\angle g$, $\angle b$ y $\angle h$. Estos ángulos son suplementarios.

Autoevaluación

De acuerdo a la clasificación de los ángulos selecciona los valores de los ángulos marcados con $x$.